Big-O notation and complexity(big-O 표기법과 복잡도)
디스크에 있는 파일을 다른 지역의 친구에게 보낸다고 해보자. 대부분의 사람이, 이메일이나 FTP와 같은 network방식을 떠올리게됩니다.
하지만 파일의 크기가 1TB라면? 이럴때는 자동차를 타고 직접 전달하는게 빠르지 않을까?
이렇게 어떤 행위(컴퓨터에선 알고리즘을 의미)에 대한 비용을 어떻게 비교할까요?
여기선 컴퓨터에서 효율성을 비교하는 방법을 알아보겠습니다.
big-O의 의미
big-O 시간은 알고리즘의 효율성을 나타내는 지표(metric) 혹은 언어입니다. 이를 통해 알고리즘이 이전보다 빨라졌는지 느려졌는지 판단합니다.
시간복잡도(time complexity)
big-O표기법에 따른 그래프
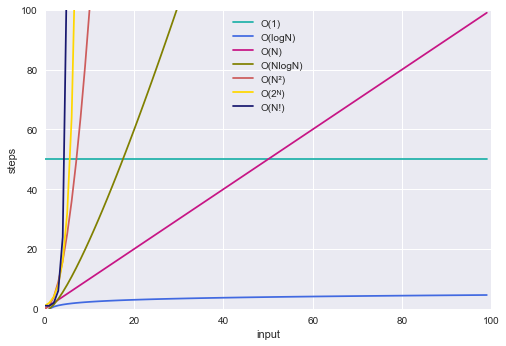
위의 그래프처럼 다양한 big-O표기가 있습니다.
O(1)(상수의 시간복잡도)가 얼마냐에 따라, 특정 input범위에선, O(1)의 시간복잡도가 더 클 수 있습니다.
big-O, big-θ, big-Ω
big-O(big-O)(최악의 경우) 엄밀히 말하면(그리고 학계에선) big-O는 시간의 상한을 나타냅니다. 또 다른 말로, ‘최악의 경우’를 나타냅니다.
예를 들면, array의 모든 값을 std console(표준 출력, console창)에 출력한다면, O(N)으로 표현할 수 있지만, 이 외에 $O(N^2), O(N^3), O(2^N)$도 옳은 표현입니다.하지만, 업계에선 ‘big-O’를 ‘big-θ’의 의미를 추가하여 사용하고 있습니다. 이 부분이 ‘학계에선’이라고 표현한 이유입니다.
big-Ω(big-Omega)(최선의 경우) 학계에선 big-Ω는 최선(best)의 상황에 대한 표기입니다.
예를 들어, array의 모든 값을 출력하는 상황은 Ω(N) 뿐만 아니라 $\Omega{(\log{N})}$ 혹은 $\Omega{(1)}$로 표현할 수 있습니다.Q: 위의 array예시(모든 값을 출력하는)에서, $\Omega(\log{N})$, $\Omega{(1)}$이 가능할까?
A: 불가능합니다. 모든 array의 element(구성요소)들을 최소 1회 읽어야 합니다.
big-θ(big-theta)(딱 맞게 표현하고 싶은 경우)
big-O와 big-Ω 모두를 의미합니다.
예를 들어, 어떤 알고리즘이 O(N)이면서 Ω(N)이라면, 이 알고리즘을 θ(N)으로 표기할 수 있습니다.최선의 경우(big-Ω)는 별로 쓸만한 개념이 아닌 탓에 논의 대상이 되지 않는다. 아무 알고리즘에 대해서 최선에 해당되는 특수한 input을 넣는다면, O(1)에 동작하도록 만들 수 있다. 대부분의 경우 최악의 경우(big-O)에 관심이 있기 때문에, big-O로 표기하곤 한다.
공간복잡도(space complexity)
알고리즘의 공간 측면에서의 복잡도 입니다.
시간복잡도와는 완전히 구분되며, 크기가 n인 배열을 만든다면 O(n)으로, n x n 배열을 만든다면, $O(n^2)$으로 공간복잡도를 표기합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 예제 1
int sum(int n) {
if (n <= 1){
return 0;
}
return n + sum(n-1);
}
// 예제 2
int pairSumSequence(int n) {
int sum = 0;
for (int i=0; i < n; i++) {
sum += pairSum(i, i + 1);
}
return sum;
}
int pairSum(int a, int b) {
return a + b;
}
- 예제 1의 경우
- O(n)의 시간복잡도와 O(n)의 공간복잡도를 갖습니다.
- 공간복잡도가 O(n)인 이유는, function call이 call stack에 n개 쌓이기 때문입니다. 이 function call또한 memory의 공간을 차지합니다.
- 단순히 function call을 n번했다고, O(n)의 공간을 사용하지는 않습니다.
- 공간복잡도가 O(n)인 이유는, function call이 call stack에 n개 쌓이기 때문입니다. 이 function call또한 memory의 공간을 차지합니다.
- 예제 2의 경우를 보면,
- 예제 1과 같이 총 n번 호출하지만, 각 function이 모두 종료(이 과정에서 memory free가 발생하기 때문)된 후 실행되므로, O(1)의 공간을 사용한다.
n번 iteration을 수행하기 때문에 O(n)의 공간복잡도를 갖는다고 생각할 수 있지만, n의 증가와 상관없이 상수(constant number)의 공간복잡도(O(1))을 갖기 때문에, O(1)이 맞습니다. big-O는 단순히 증가하는 비율을 표현합니다
big-O 표기법의 기본적인 규칙들
상수항(constant value)는 무시한다.
big-O는 단순히 증가하는 비율을 나타냅니다. 특정 input데이터 안에서 $O(N)$이 $O(1)$보다 작은경우가 있지만(참고), ‘증가하는 비율’을 비교하고자 함으로, 상수는 생략하게 됩니다.
이에 따라, 2개의 연속된 iteration(반복)구문(for, while등) 같은 경우$O(2N)$이 아닌 $O(N)$으로 표기합니다.
$O(N)$이 항상 $O(2N)$보다 낫지는 않습니다. 이런일이 발생하는 이유는, 실제로 CPU에 전달되는 명령어(assembly어)가 내부 연산(+,* 등)에 따라 차이가 있기 때문입니다.
지배적이지 않은 항은 무시하라(가장 영향력이 큰것만 표시한다)
- $O(N^2+N)$은 $O(N^2)$으로
- $O(N+\log{N})$은 $O(N)$으로
- $O(5*2^{N}+1000N^{100})$은 $O(2^N)$으로
표기합니다.
N의 모수(parameter)가 아예 다른경우($O(B^2+A)$와 같은 경우)는 줄일 수 없습니다.
](/assets/img/for-post/big-O and Time Complexity/image%201.png)
big-O의 N크기에 따른 연산차이를 표현한 graph. 그 성능에 따라 horrible~excellent까지 추가로 표기되어 있습니다. 출처: https://www.bigocheatsheet.com/
여러 단계로 이루어진 알고리즘은 어떻게 표현할까?
실제로, 알고리즘은 여러 단계의 연산을 거치게 됩니다. 이럴때 시간 복잡도를 어떻게 표현해야 할까요?
1
2
3
4
5
6
7
8
// O(A + B)
for (int a: arrA) {
print(a);
}
for (int b: arrB) {
print(b)
}
1
2
3
4
5
6
// O(A * B)
for (int a : arrA) {
for (int b : arrB) {
print(a + " " + b)
}
}
Amortized Time(Amortized Analysis, 분할 상환 분석)
알고리즘이, 상황에 따라 아주 나쁜 시간복잡도를 갖지만, 보통의 경우는 또 다른 시간복잡도를 갖는경우 표현하는 방법에 대해서 알아봅니다.
Java의 ‘ArrayList’예시
Java의 ‘ArrayList’는 ‘dynamic size array(동적으로 array크기가 바뀌는)’입니다. 즉, array이지만, 배열의 크기가 자유롭게 조절됩니다.
‘ArrayList’는 배열의 크기가 가득찼을때,
- 기존보다 2배 더 큰 array를 만든뒤
- 이전 array의 모든 요소(element)를 새 array로 copy합니다.
이런 spec을 기준으로, ‘ArrayList’의 삽입(insert)연산의 시간복잡도(Time Complexity)는 어떻게 될까?
2가지 상황으로 나누어서 생각할 수 있습니다
- array가 꽉찬 경우(배열 요소가 N개인 경우):
- 새로운 element를 만들기 위해, 2N크기의 array를 생성하고, 기존 array에서 N개의 element를 copy해야 하므로, 이 경우
- $O(N)$이 됩니다.
- array가 비어있는 경우:
- 배열에 이미 공간이 있기 때문에,
- $O(1)$이 됩니다.
이에 따라 최악의 경우인 $O(N)$으로 표기하는게 맞을까요?
그러나, 최악의 경우(array가 꽉찬경우)에 마주하는 경우는 극히 드물기 때문에, 실제의 시간복잡도를 온전히 반영하고 있지 않습니다.
이에 따라, 이 최악의 경우($O(N)$인 경우)를 분할해서, 다른 상황에 할당하는 방식으로 계산합니다.
계속해서 ArrayList의 예시를 이어가면,
ArrayList는 1, 2, 4, 8, 16, …, X처럼 $2^n$크기 일때, 최악의 경우($O(N)$)가 발생한다.
이때, X개의 element를 삽입한다면, 총 시간복잡도는 $1+2+4+8+16+\dots+X$이 됩니다.
이를 거꾸로 뒤집어서 생각하면, X부터 $\frac{1}{2}$씩 줄어든다고 볼 수 있습니다. 이를 적용하면,
로, 2X(근사값으로서)가 됩니다.
이에 따라, X개의 원소를 모두 삽입(insert)할때 필요한 시간은 $O(2X)$이고,
이를 분할하여, 1회 삽입(insert)에 드는 시간은 $O(1)$입니다.
$\log{N}$ runtime
많은 알고리즘에서, $\log{N}$의 시간복잡도(time complexity)를 갖고 있습니다. 이 $\log{N}$은 어떻게 구해진걸까요?
Binary Search Tree(BST, 이진 탐색 트리)
](/assets/img/for-post/big-O and Time Complexity/image%202.png)
binary search tree 예시 출처: https://en.wikipedia.org/wiki/Binary_search
‘Binary Search Tree(BST)’는 특정 element를 찾을때, 그 탐색 대상을 절반($\frac{1}{2}$)씩 줄여나갑니다.
예를 들어, 탐색 대상(N)이 총 16개인 경우($N = 16$),
$N=16$(첫번째 탐색대상)
$N=8$(두번째 탐색대상)
$N=4$(세번째 탐색대상)
$N=2$(네번째 탐색대상)
$N=1$(다섯번째 탐색대상, 찾음)
로 탐색 대상이 각 단계 마다 $\frac{1}{2}$씩 줄어듭니다. 이를 거꾸로 뒤집으면, 마지막으로 부터 2배씩 증가한다고 볼 수 있습니다.
이때, ‘탐색 횟수’가 시간복잡도에 해당되며, 이는 $2^{k} = N \text(k는 실행횟수)$를 만족하는 k를 찾는것과 같습니다.
이렇게 실행횟수 k는 $\log_2{N}$이 됩니다.
이 BST와 같이 알고리즘의 대상이 $\frac{1}{2}$씩 줄어든다면, 해당 알고리즘의 시간복잡도는 $\log{N}$일 가능성이 높습니다.
big-O표기에서는 상수항은 무시하기 때문에, $\log_2$의 밑에 해당하는 ‘2’는 생략하고 표시합니다. 즉, $\log(N)$으로 표기합니다.
Recursive runtime(재귀호출 수행시간)
Recursive 알고리즘 같은경우, 시간복잡도(time complexity)를 구하기 까다롭습니다.
1
2
3
4
5
6
int f(int n) {
if (n <= 1) {
return 1;
}
return f(n - 1) + f(n - 1);
}
위와 같은 함수가 있을때, 성급하게 $O(N^2)$라고 할 수 있지만(f가 2회 호출되기 때문에), 이는 잘못된 답입니다.
이 function을 수행하는 과정을 그려보면, 아래와 같이 tree형식으로 표현할 수 있습니다.
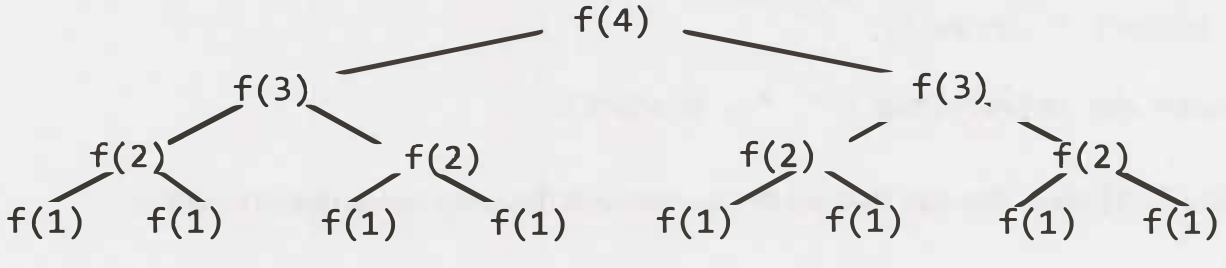
이때, function call에 해당하는 ‘Node의 갯수’와 ‘tree의 깊이(depth)’의 관계는 아래와 같이 표현됩니다.
| 깊이(depth) | 노드의 갯수(function call 횟수) | 다르게 표현하면 | 또 다른 표현 |
|---|---|---|---|
| 0 | 1 | 2^0 | |
| 1 | 2 | 2 * 이전 깊이 | 2^1 |
| 2 | 4 | 2 * 이전 깊이 | 2^2 |
| 3 | 8 | 2 * 이전 깊이 | 2^3 |
| 4 | 16 | 2 * 이전 깊이 | 2^4 |
이렇게 각 layer마다 node의 갯수는 $2^{depth}$가 됩니다.
시간복잡도(Time complexity)는 이 node갯수의 총 합에 해당하므로,
즉 시간복잡도(Time complexity)는
\[O(2^{N})\]이 된다.
recursive함수에서, 시간복잡도는 보통 $O(\text{분기 갯수}^{깊이})$로 표현됩니다.
공간복잡도는 $O(N)$인데,
이는 특정 시각에 사용하고 있는 공간의 크기가 $O(N)$이기 때문입니다.
Recursive Algorithm의 최적화
Recursive Algorithm의 경우, 단순히 ‘recursion’만 적용하면, $O(2^{n})$의 Time complexity(시간복잡도)를 갖게 됩니다.
1
2
3
4
5
6
7
fn fibonacci(n: u32) -> u32 {
if n <= 1 {
return n
}
return fibonacci(n-1) + fibonacci(n-2)
}
하지만, fibonacci 처럼, 같은 계산을 중복으로 실행해야하는 경우가 많은 Algorithm은, 이 결과 값을 저장(cache)함으로서 성능을 개선할 수 있습니다.
이 경우, Time Complexity(시간복잡도)를 $O(n)$으로 줄일 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 메모이제이션을 적용한 피보나치 함수
fn fibonacci_memo(n: u32, memo: &mut HashMap<u32, u32>) -> u32 {
if let Some(&result) = memo.get(&n) {
return result;
}
let result = if n <= 1 {
n
} else {
fibonacci_memo(n - 1, memo) + fibonacci_memo(n - 2, memo)
};
memo.insert(n, result);
result
}
fn main() {
let mut memo = HashMap::new();
let n = 10; // 계산할 n 값
let result = fibonacci_memo(n, &mut memo);
println!("Fibonacci({}) = {}", n, result);
}