Vector Similarity Explained(Vector의 유사도를 측정하는 방법에 관하여)

목적

‘vector embedding’은 NLP와 computer vision에서 그 효과를 입증했습니다.
여기서는 이 ‘vector embedding’을 비교(check similarity)하여 metric으로 만드는 3가지 방법을 알아봅니다.

Euclidean distance

‘Euclidean distance’는 두개의 vector사이의 거리를 측정하는 방법입니다.

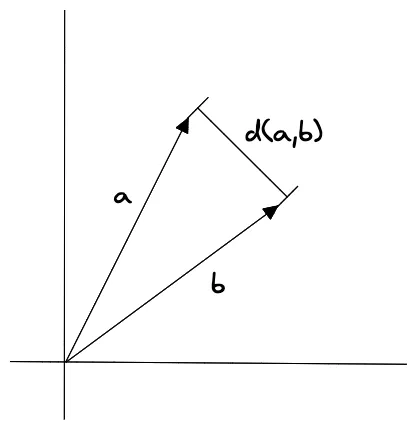
기존에 알고 있던, 유클리드 좌표기반의 ‘두점사이의 거리’를 구하는것과 같습니다.

\[d(a,b)= \sqrt{(a_1​−b_1​)^2+(a_2​−b_2​)^2+...+(a_n​−b_n​)^2​}\]

이렇게 \(a_1,b_1\)부터 \(a_n,b_n\)까지의 모든 component(vector의 property)들을 계산해야합니다.

sensitive to scale

이 ‘Euclidean distance’는 vector의 크기(절대값)에 영향을 많이 받습니다. 즉, 크기가 큰 vector들의 ‘euclidean distance’의 값이 작은 vector들의 값보다 큽니다. 2개의 vector가 유사하게 보여도, ‘euclidean distance’에선 차이를 보입니다. ‘Euclidean distance’는 문자 그대로, vector사이의 거리를 구하는 것이기 때문에, 매우 직관적인 metric입니다.

이 ‘Euclidean distance’가 작다면, 실제로 두 vector의 거리가 아주 가깝다는것을 의미합니다. 이는 밑에 기술할, ‘Dot product’와 ‘Consine’ 일반적인(generally) 사실(true)이 아닙니다.

ML에서의 평가

DLM(deep learning model)에서는 자주 쓰지 않습니다.
가장 기본적인 vector encoding 도구인 LSH (Locality Sensitive Hashing)같은곳에서 사용하고 있습니다.
또, model을 train하는 과정에서, 특별히 정해진 loss function이 없다면 사용되곤 합니다.(직관적이라 접근성이 좋아서 자연스럽게 사용하게 된다는 뜻)

‘Euclidean distance’가 vector크기에 민감(sensitive)하다는 면 때문에, 대상의 갯수나 크기가 정보가 데이터(training set과 같은 학습용 데이터)에 포함되어야 할때 사용되곤 합니다.
예를 들면, 유저의 이전 구매이력을 기초로하는 추천시스템(recommendation system)과 같은것이 그렇습니다.
이때는, 이미 구입한 상품과 절대적 거리를 측정하는 방법을 사용합니다.

Dot product Similarity(vector 내적)

vector의 dot product를 metric으로 사용하는 방법입니다.
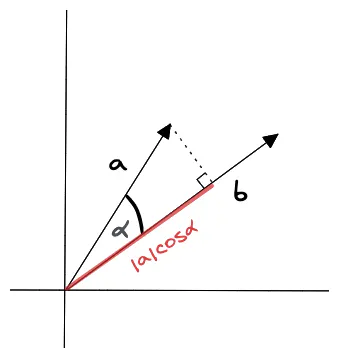
‘dot product’를 계산하는 방법은 아래와 같이 2가지 방법이 있습니다. 여기선, 2번째 방법인, vector의 크기와 cosine을 이용한 방법을 사용합니다.

\[a⋅b=\sum_{\substack{i=1}}^n{a_{i}b_{i}}=a_{1}b_{1}+a_{2}b_{2}+…+a_{n}b_{n}\] \[a⋅b=∣a∣∣b∣\cos{\alpha}\]

‘Dot product’의 결과 값은 scalar값입니다(vector가 아닙니다).

\(\alpha\)가 90도 미만이면 +(positive) 값을 갖고,

90도보다 크다면, -(negative) 값을 갖고,

90도(수직, orthogonal)이면, 0이 됩니다.

이는 \(\cos{\alpha}\)에 따라 값이 바뀌는것을 말합니다.

‘Dot product’는 두 vector의 크기(length)와 방향(direction)모두에게 영향을 받습니다.

만약, 2개의 vector가 크기는 갖고,

방향이 반대(opposite)인 것보다,

방향이 동일한것이 더 큽니다.

ML에서의 평가

LLMs(Large Language models)와 같은 곳에서 자주 보게 됩니다.
고도화된 추천시스템(recommender system)에서도 사용하게 됩니다.
이 고도화된 시스템에선, 모든 유져(user)와 상품(item)이 ‘embedding’되어 있으며, model이 ‘user embedding’과 ‘item embedding’의 ‘dot product’를 학습하여 좋은 성능(item과 user의 매칭정도를 측정할때의 성능)을 내게 됩니다.
만약 2개의 product가 같은 방향을 가리키지면, 다른 크기(magnitude)를 갖고 있다면, 이 2개의 상품은 같은 topic을 갖고 있지만, vector의 크기가 큰 상품을 더 좋게 평가합니다.

Cosine Similarity

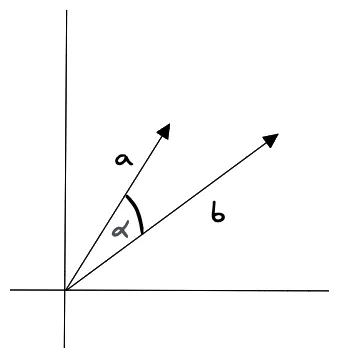
‘Cosine Similarity’는 2개의 vector사이의 각도(angle)을 metric으로 사용하는 방법입니다.
이 ‘Cosine Similarity’는 vector의 크기에 영향을 받지않고, 오직 각도(angle) 혹은 방향(direction)에만 영향을 받습니다.

\[\text{sim}(a,b)=\frac{a\cdot{b}}{\|a\|\cdot{\|b\|}}\]

‘Cosine Similarity’는 -1에서 1사이의 값을 갖는다.

1은 $\alpha$가 0이라는 뜻이고,

0은 수직(orthogonal)

-1은 2개의 vector가 완전히 반대방향이라는 뜻입니다.

만약, 이 ‘Cosine Similarity’을 사용한 model을 사용하고 있다면, 동일하게 사용해줘야 합니다. 또한, ‘normalize와 dot product’를 조합한것도 수학적으로 동일하기 때문에, 가능합니다.
어떤 경우에는 ‘normalize후 dot product하는 것’이 더 나을때가 있고, ‘cosine similarity’가 나을때도 있습니다.

ML에서의 평가

‘Cosine similarity’는 ‘semantic search(의미를 통한 검색)’과 ‘document classification problems’에서 사용합니다. 이는 ‘cosine similarity’가 2개의 vector의 방향성만 비교하는 특징을 이용한것입니다.
유사하게, ‘recommendation system’에서 유저의 과거 행동기록을 기반한 상품을 추천할때도 사용할 수 있습니다.
반면에, magnitude(크기, 량) of vector’가 중요하고, 반드시 이 값이 ‘similarity’에 반영되어야 하는 경우에는 적합하지 않습니다.
예를 들면, pixel intensities에 기반한 ‘image embeddings’ 유사도 비교와 같은 경우가 있습니다.

Wrap-up

Model이 train할때 사용한 ‘Similarity’ metric과 동일한 metric을 사용하는것이 중요합니다.
만약, model에서 사용된 metric을 모른다면, 여러 metric중에 적당한걸 찾기위해 여러 실험을 거칠필요가 있습니다.

Reference

Vector Similarity Explained

Different types of Distances used in Machine Learning

이미지 자료 출처

Vector Similarity Explained