LeetCode 75-13 Max Number of K-Sum Pairs

문제 요약

integer array인 nums안에서, 그 합이 k를 만족하는 2개의 요소를 구합니다.

• 이때, k를 만족하는 요소는 중복으로 사용될 수 없습니다.

문제 풀이

첫번째 시도

Complexity

시간복잡도(time complexity) 는 $O(n\log{k})$입니다. 이는 nums를 정렬(sort)하는 과정이 있기 때문입니다.
공간복잡도(space complexity) 는 $O(n)$입니다. 주어진 nums가 ‘immutable(불변)’ 상태임으로, nums를 copy하는 저장공간이 추가로 필요합니다.

왼쪽(nums 시작점)에서 출발하는 pointer와 오른쪽(nums 끝)에서 출발하는 pointer, 총 2개의 pointer를 이용합니다.
여기서, pointer를 변경하는 부분이 중요한데, 이 pointer변경을 단순하게 하기 위해서, ‘nums’를 오름차순으로 정렬(sort)해야 합니다.

정렬된 ‘nums’는 다음과 같은 조건을 만족합니다.

left_pointer는 커질수록 element값도 커집니다.

right_pointer는 작아질수록 element의 값도 작아집니다.

이에 따라, left_pointer와 right_pointer가 가리키는 element의 합(sum)을 k와 비교해서 pointer를 변경합니다.

sum이 k보다 크면, 값을 작게 만들어야 합니다. 때문에, right_pointer를 왼쪽으로 이동합니다.

sum이 k보다 작으면, 값을 크게 만들어야 합니다. 이에따라, left_pointer를 오른쪽으로 이동합니다.

fn max_operations_v1(nums: Vec<i32>, k: i32) -> i32 {
    let mut sorted_nums: Vec<i32> = nums.clone();
    sorted_nums.sort();

    let mut left_pointer: usize = 0;
    let mut right_pointer: usize = sorted_nums.len() - 1;

    let mut count = 0;
    while right_pointer > left_pointer {
        let left_element = sorted_nums[left_pointer];
        let right_element = sorted_nums[right_pointer];

        let sum = left_element + right_element;

        if sum == k {
            count += 1;
            left_pointer += 1;
            right_pointer -= 1;
        } else if sum < k {
            left_pointer += 1;
        } else {
            right_pointer -= 1;
        }
    }


    return count;
}

fn main() {
    assert_eq!(max_operations_v1(Vec::from([1,2,3,4]), 5), 2);
    assert_eq!(max_operations_v1(Vec::from([3,1,3,4,3]), 6), 1);
}

결과

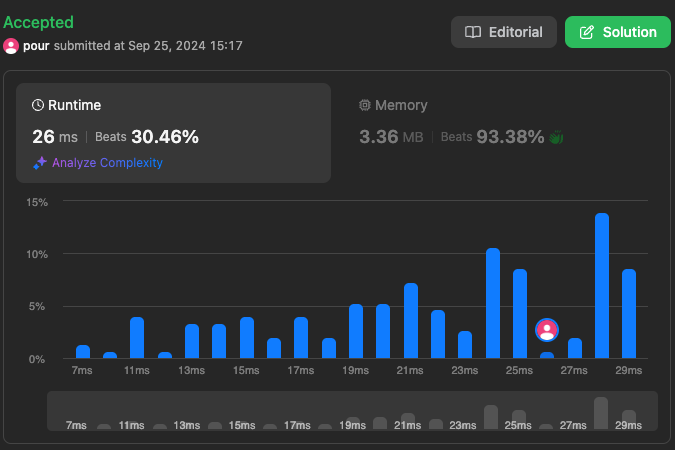
Leetcode 제출 결과

두번째 시도

Complexity

시간복잡도(time complexity) 는 $O(n\log{n})$입니다.
공간복잡도(space complexity) 는 $O(n)$입니다.

nums의 sort 알고리즘을 ipnsort를 사용하도록 바꾸었으며, nums의 길이가 0인 경우 함수가 빨리 종료되도록 변경하였습니다

ipnsort는 ‘quick sort’의 average case와 ‘heap sort’의 (빠른) worst case를 합친, 즉 장점을 합친 알고리즘이라고 합니다.
rust 공식문서에서 ‘sort_unstable’ 참고

fn max_operations_v2(nums: Vec<i32>, k: i32) -> i32 {
    let mut sorted_nums: Vec<i32> = nums.into_iter().filter(|val| val < &k).collect::<Vec<i32>>();

    if (sorted_nums.len()==0){
        return 0
    }

    sorted_nums.sort_unstable();

    let mut left_pointer: usize = 0;
    let mut right_pointer: usize = sorted_nums.len() - 1;

    let mut count = 0;
    while right_pointer > left_pointer {
        let left_element = sorted_nums[left_pointer];
        let right_element = sorted_nums[right_pointer];

        let sum = left_element + right_element;

        if sum == k {
            count += 1;
            left_pointer += 1;
            right_pointer -= 1;
        } else if sum < k {
            left_pointer += 1;
        } else {
            right_pointer -= 1;
        }
    }


    return count;
}

fn main() {
    assert_eq!(max_operations_v2(Vec::from([1,2,3,4]), 5), 2);
    assert_eq!(max_operations_v2(Vec::from([3,1,3,4,3]), 6), 1);
}

결과

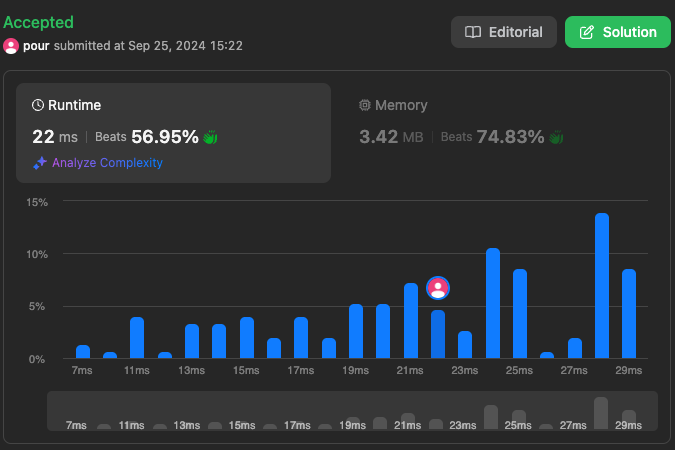
Leetcode 제출 결과

References

Max Number of K-Sum Pairs - LeetCode